# 1.1 性能概述
为什么程序总是那么慢?它现在到底在干什么?时间都花在哪里取了?也行,你经常会抱怨这些问题。如果是这样,那说明你的程序出了性能问题。和功能性问题相比,性能问题在有些情况下,可能并不算什么太大的问题,将就将就,也就过去了。但是,严重的性能问题会导致程序瘫痪、假死,直至崩溃。本节就先来认识性能的各种表现和指标。
# 1.1.1 看懂程序的性能
对客户端程序而言,拙劣的性能会严重影响用户的体验,界面停顿、抖动、响应迟钝等问题会遭到用户不停的抱怨。一个典型的例子就是 Eclipse IDE 工具在Full GC的时候会出现程序假死的现象,相信一定被不少开发人员所诟病。对于服务器程序来说,性能问题则更为重要,相信不少后台服务器软件都有各自的性能目标。以Web服务器为例,服务器的响应时间、吞吐量就是两个重要的性能参数。当服务器承受巨大的访问压力时,可能出现响应时间边长‘、吞吐量下降,甚至是抛出内存溢出异常而崩溃。这些问题,都是性能退遨游需要解决的。
一般来是,程序的性能通过一下几个方面来表现:
- 执行速度:程序的反应是否迅速,响应时间是否足够短。
- 内存分配:内存分配是否合理,是否过多的消耗内存或者存在泄漏。
- 启动时间:程序从运行到可以正常处理业务需要花费多长时间。
- 负载承受能力:当系统压力上升时,系统的执行速度、响应时间的上升曲线是否平缓。
# 1.1.2 性能的参考指标
为了能够科学的进行性能分析,对性能指标进行定量评测是非常重要的。目前,一些可以用于定量评测的性能指标有:
- 执行时间:一段代码从开始运行到运行结束,所使用的时间。
- CPU时间:函数或者线程占用CPU的时间。
- 内存分配:程序再运行时占用的内存空间。
- 磁盘吞吐量:描述I/O的使用情况。
- 网络吞吐量:描述网络的使用情况。
- 响应时间:系统对某用户行为或者时间做出响应的时间。响应时间越短,性能越好。
# 1.1.3 木桶原理与性能瓶颈
木桶原理又称“短板理论”,其核心思想是:一只木桶盛水的多少,并不取决于桶壁上最高的那块木块,二十取决于桶壁上最短的那块,如果1.1所示:

将这个理论应用到系统性能优化上,可以这么理解,及时系统拥有充足的内存资源和CPU资源,但是如果磁盘I/O性能低下,那么系统的总体性能是取决于当前最慢的磁盘I/O速度,而不是当前最优越的CPU或者内存。在这种情况下,如果需要进一步提升系统性能,优化内存或者CPU资源是好无用处的。只有提高磁盘I/O性能才能对系统的整体性能进行优化。而此时。磁盘I/O就是系统的性能瓶颈。
注意:根据木桶原理,系统的最终性能取决于系统中性能表现最差的组件,因此,为了提升系统整体性能,必须对系统中表现最差的组件进行优化,而不是对系统中表现良好的组件进行优化。
根据应用的特点不通,任何计算机资源都有可能成为系统瓶颈。其中,最优可能成为系统瓶颈的计算资源如下:
- 磁盘I/O:由于磁盘I/O读写的速度要比内存慢很多,程序再运行过程中,如果需要等待磁盘I/O完成,那么低效的I/O操作会拖累整个系统。
- 网络操作:对网络数据进行读写的情况与磁盘I/O类似。由于网络环境的不确定性,尤其是对互联网上数据的读写,网络操作的速度可能比本地磁盘I/O更慢。因此,如不加特殊处理,也极可能成为系统瓶颈。
- CPU:对计算资源要求较高的应用,由于期长时间、不间断的大量占用CPU资源,那么对CPU的争夺将导致性能问题。如科学计算、3D渲染等对CPU需求旺盛的应用。
- 异常:对Java应用来说,异常的捕获和处理是非常消耗资源的。如果程序高频率的进行异常处理,则整体性能便会有明显下降。
- 数据库:大部分应用程序都离不开数据库,而海量数据的读写操作可能是相当费时的。而应用程序可能需要等待数据库操作完成或者返回请求的结果集,那么缓慢的同步操作将成为系统瓶颈。
- 锁竞争:对高并发程序来说,如果存在激烈的锁竞争,无疑是对性能极大的打击。锁竞争将会明显增加线程上下文切换的开销。而且,这些开销都是与应用需求无关的系统开销,白白占用宝贵的CPU资源,却不带来任何好处。
- 内存:一般来说,只要应用程序设计合理,内存在读写速度上不太可能成为性能瓶颈。除非应用程序进行了高频率的内存交换和扫描,但这些情况比较少见。使内存制约系统性能的最可能情况是内存大小不足。与磁盘相比,内存的大小似乎小的可怜,这意味着应用软件只能尽可能将常用的核心数据读入内存,这再一定程度上降低了系统性能。
# 1.1.4 Amdahl 定律
AmdahI 定律是计算机科学中非常重要的定律,它定义了串行系统并行化后加速比的设计公式和理论上限。
加速比定义:加速比 = 优化前系统耗时/优化后系统耗时
所谓加速比,就是优化前的耗时与优化后的系统耗时的比值。加速比越高,表明优化效果越明显。
Amdahl定律给出了加速比与系统并行度和处理器数量的关系。设加速比为 Speedup,内存必须串行化的程序比重为F,CPU处理器数量为N,则有:
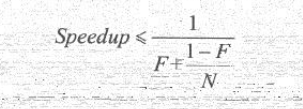
根据这个公式,如果CPU处理器数量趋于无穷,那么加速比与系统的串行化率成反比,如果系统中必须有50%的代码串行执行,那么系统的最大加速比为2。
假设有一程序分为一下步骤执行,每个执行步骤花费100个时间单位。其中,只有步骤2和步骤5可以进行并行,步骤1、3、4必须串行,如图1.2所示。在全串行的情况下,系统合计耗时500个时间单位。

若将步骤2和步骤5并行化,假设在双核处理上,则有如果1.3所示的处理流程。在这种情况下,步骤2和步骤5的耗时将为50个是单位。故系统整体耗时为400个时间单位。根据加速比的定义有:加速比 = 优化前系统耗时/优化后系统耗时 = 500/400 = 1.25 。或者前文中给出的加速比公式。由于5个步骤中,3个步骤必须串行,因此其串行化比重为3/5=0.6,即F=0.6,且双核处理器的处理器个数N为2.带入公式得:加速比 = 1/(0.6+(1-0.6)/2)=1.25
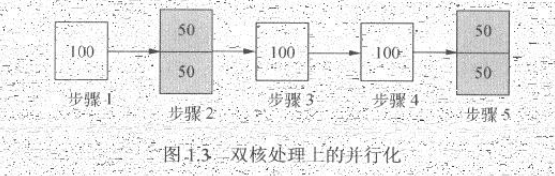
在极端情况下,假设并行处理器个数为无穷大,则有如图1.4所示的处理过程。步骤2和步骤5的处理时间趋于0。即使这样,系统整体耗时依然大于300个时间单位。即加速比的极限为500/300=1.67。
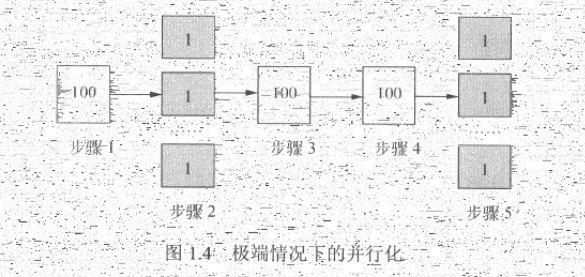
使用加速比计算公式,N趋于无穷大,有Speedup=1/F,且F=0.6,故有Speedup=1.67。由此可见,为了提高系统的速度,仅增加CPU处理器的数量并不一定能起到有效的作用,需要从根本上修改程序的串行行为,提高系统内可并行化的模块比重,在此基础上,合理增加并行处理器数量,才能以最小的投入,得到最大的加速比。
注意:根据Amdahl定律,使用多核CPU对系统进行优化,优化的效果取决于CPU的数量以及系统中的串行化程序的比重。CPU数量越多,串行化比重越低,则优化效果越好。仅提高CPU数量而不降低程序的串行化比重,也无法提高系统性能。